Rescaled range analysis, or RRA, is one of the many techniques used to examine and forecast the movements of economic indicators and financial assets. In contrast to various other methods, RRA can be applied to all kinds of data series regardless of their statistical properties. It can be viewed as a major advantage, as in most cases financial data does not meet the strict requirements of forecasting models.
In this research we examine the implications of RRA and the ways how to use the information it gives in practice.
In finance, RRA is used to study mean reversion and mean aversion in the process of price development. It is more commonly applied to stock market, but methodologically there are no restrictions against employing it for investigating exchange rates. Therefore we use RRA to try and classify the behaviour of two major currency pairs – EUR/USD and USD/JPY, - and two crosses – EUR/CHF and GBP/JPY. The datasets are formed from ten minute, one hour and one day candles up to August 2013.
Methodology
The main purpose of rescaled range analysis of a process is to estimate its Hurst exponent – a measure of the so called long-term memory. The notion of the Hurst exponent comes from an idea about dependence between certain characteristics of the process and a time span over which they are observed.
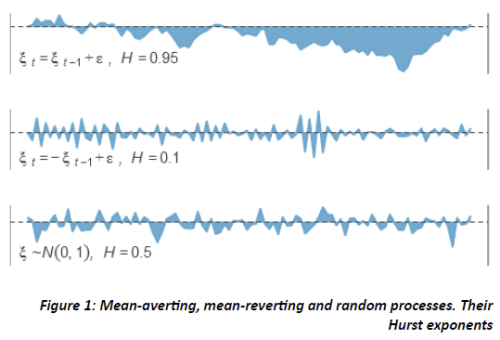
Results
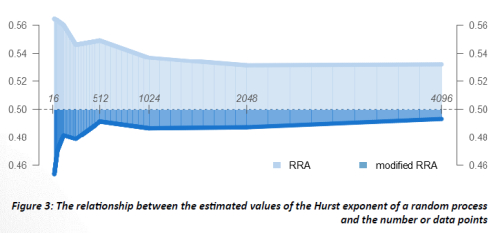
1. Modified RRA gives more accurate results for random processes.
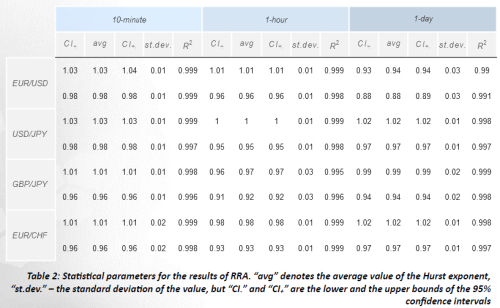
2. RRA classifies all examined exchange rates as strongly trending.
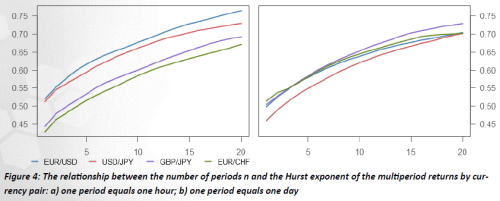
3. RRA shows a direct relationship between time-separated returns.

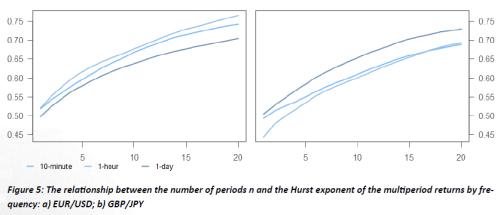
Conclusions
We studied two methods of estimating the Hurst exponent – the measure of long-term memory in a process. We saw that classical rescaled range analysis, which is one of the most commonly used means for estimating the parameter, and its modified version both have their own flaws. Classical RRA proved to overestimate the Hurst exponent, while the modified method, on the contrary, produced underestimated values. However, modified RRA gave a lesser error of estimation, and thus seemed to be more accurate.
All examined exchange rate had high values of the Hurst exponent, indicating a tendency to follow persistent trends. In most cases these high values were supported by relatively high ADX. We also saw that against the background of the high values of the Hurst exponent the existing trends most often preserve their direction and strength for some period in future. However, the analysis of the exchange rates did not give any values of the Hurst exponent equal to or lesser than 0.5, while there were plenty of cases of the small values of ADX. Therefore it is hard to make assumptions about a relationship between the results of RRA and more popular measures of describing trends.
RRA provided some new insight into the behaviour of currency pair returns. It appeared that there is a direct relationship between multiperiod logarith-mic returns, and that it strengthens with increasing periods. Results show that the sets of ten- and more period returns have a Hurst exponent high enough to classify them as persistent. This denies the pure randomness of the development of currency pair returns and suggests that there might be fairly efficient methods for modelling the returns and thus forecasting future moves.

